4y 8 2y 5 0

Given: #2y^2+4y+x-eight=0#

To write in standard form, we add together #-2y^2-4y+8# to both sides:

#10 = -2y^2-4y+8#

The above is standard class where #a = -2#, #b = -4#, and #c = viii#

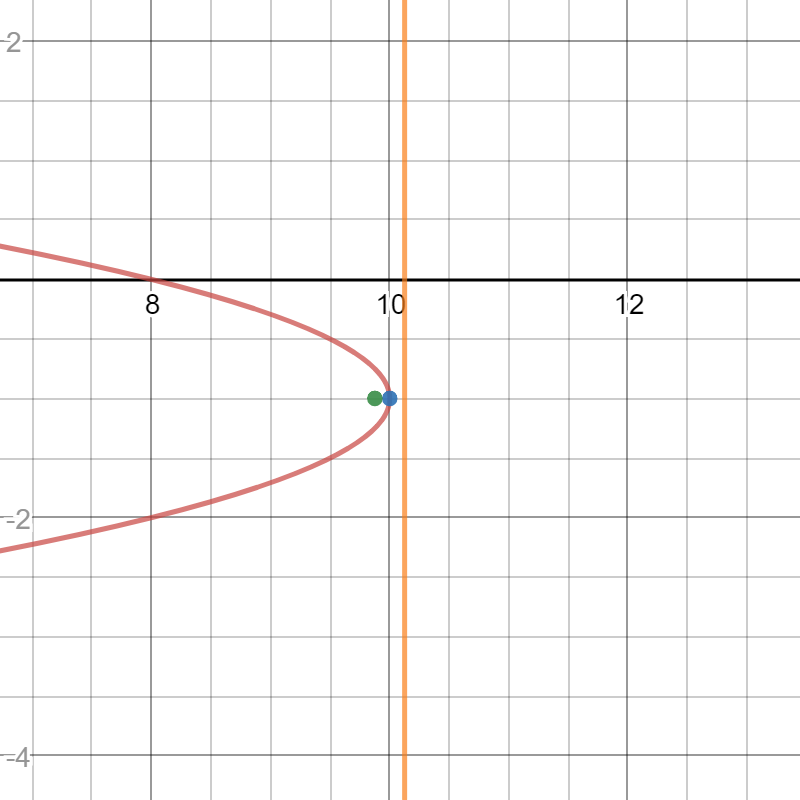
The vertex is a point #(h,k)#

The formula for the y-coordinate of the vertex is:

#k = -b/(2a)#

Substitute in the values, #a = -2# and #b = -4#

#k = -(-four)/(two(-2)#

#one thousand = -1#

The formula for the 10-coordinate of the vertex is:

#h = ak^2+b(k) + c#

Substitute in the values, #h = -1#, #a = -2#, #b = -iv#, and #c = viii#

#h = -2(-ane)^2-4(-one) + 8#

#h =10#

The vertex is #(10,-1)#

The focal distance #f# is:

#f = ane/(4a)#

#f = ane/(four(-2))#

#f = -one/8#

The formula for the focus is:

#(h+f, k)#

Substitute in values #h = 10#, #f = -1/8#, and #thousand = -ane#

#(10-one/8, 10)#

The focus is #(79/8, -1)#

The formula for the equation of the directrix is:

#ten = h-f#

Substitute in values #h = 10# and #f = -ane/8#:

#x = 10 - -1/8#

#x = 81/8#

The above is the equation of the directrix.

The following is a drawing of the parabola, the vertex, the focus, and the directrix:

www.desmos.com/calculator

4y 8 2y 5 0,

Source: https://socratic.org/questions/how-do-you-write-the-parabola-2y-2-4y-x-8-0-in-standard-form-and-find-the-vertex